1 有限域的运算
1.1 有限域的加法
有限域上定义加法⊕:
对于两个多项式f(x)和g(x):
f(x)⊕g(x)=(f(x)+g(x))(modp(x))(modp),其中p(x)是有限域的不可约多项式,p为GF(pn)中的p为素数。
例1:
在GF(23)中:
x⊕(x2+x+1)=(x2+2x+1)(mod(x3+x+1))(mod2)
=(x2+2x+1)(mod2)
=x2+1
1.2 有限域的乘法
有限域上定义乘法⊗:
对于两个多项式f(x)和g(x):
f(x)⊗g(x)=(f(x)×g(x))(modp(x))(modp),其中p(x)是有限域的不可约多项式,p为GF(p^m)中的p为素数。
例2:
在GF(23)中:
x⊗(x2+x+1)=(x3+x2+x)(mod(x3+x+1))(mod2)
=(x2+1)(mod2)
=x2+1
2 有限域加法表和乘法表
GF(23)={0, 1, 2, 3, 4, 5, 6, 7}
={0, 1, 10, 11, 100, 101, 110, 111}
={0, 1, x, x+1, x2, x2+1, x2+x, x2+x+1}
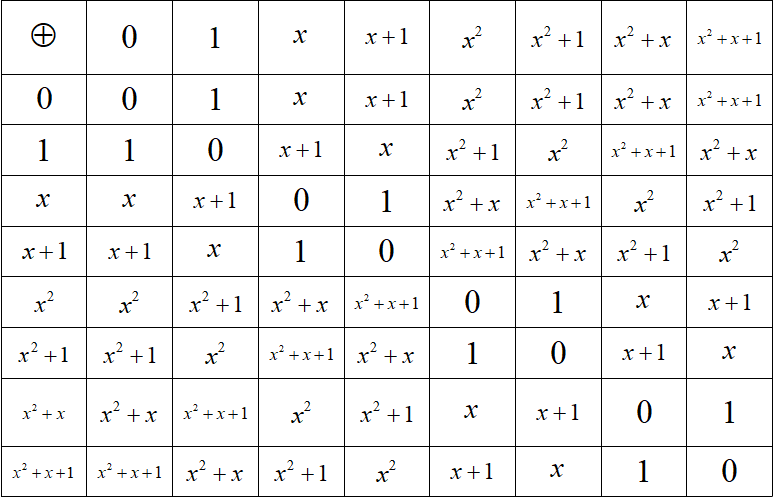
2.1 GF(23)加法表
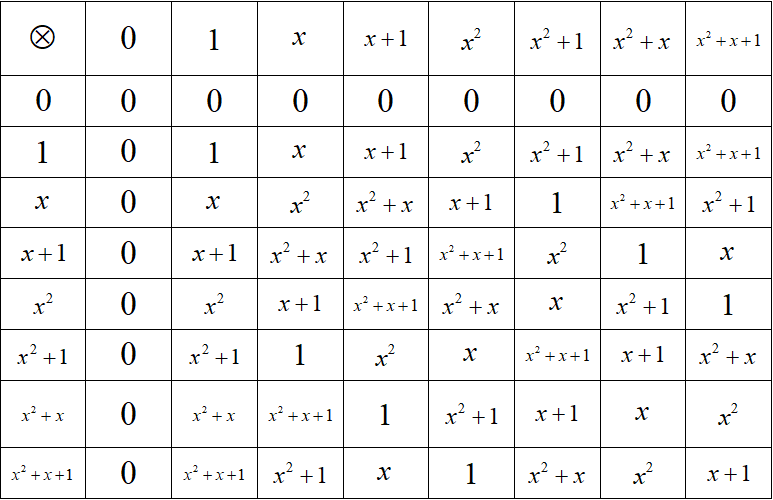
2.2 GF(23)乘法表